Механизмы
упрочнения в ВТСП - керамиках, вообще, и эффекты доменной структуры, в
частности, пока еще изучены недостаточно. Существуют лишь отдельные работы
(например, [1, 2]), посвященные теоретическим
аспектам формирования внутреннего напряженного состояния сверхпроводящей
керамики (СК), которое было бы обусловлено ее доменной структурой. Однако
быстрое развитие деструктивных процессов в изделиях СК и соответствующая
деградация сверхпроводящих свойств требуют более пристального внимания
к исследованию механизмов упрочнения, характерных для этого класса материалов.
Изучение эффектов доменной структуры в родственных керамических материалах
[3 - 6] уже показало, что она может
значительно повышать сопротивление разрушению и изменять прочностные параметры
по сравнению со случаем ее отсутствия. В поликристаллических сверхпроводящих
керамиках, испытывающих тетрагонально-орторомбический фазовый переход,
образование двойников (упругих доменов) обеспечивает уменьшение квазиоднородных
напряжений в объеме зерна. Одновременно возникают сильные неоднородные
поля напряжений, локализованные вблизи межзеренных и межфазных границ [1,
2, 7]. Вследствие анизотропии коэффициентов
теплового расширения (КТР) зерен при остывании происходит растрескивание
керамики, ухудшающее механические и прочностные свойства. В то же время,
при развитии трещины образующаяся вокруг нее зона процесса двойникования
должна приводить к экранированию трещины и повышению вязкости разрушения.
При этом релаксация внутренних напряжений 2-го рода, возникающих в СК,
может происходить двумя путями [8]:
посредством трещинообразования, характерного для температур Т <@
5000С, и мартенситного процесса перестройки доменой структуры
зерен, наиболее интенсивного при Т >@
5000С. Изучение различных механизмов упрочнения, действующих
в СК (микрорастрескивание в окрестности макротрещины, ветвление трещины
и мостикообразование за ее фронтом) уже было проведено ранее на основе
вычислительного эксперимента [9-11].
Цель настоящего исследования состоит в изучении на основе термодинамического
рассмотрения механизма упрочнения, связанного с процессами двойникования
и оценке его влияния на сопротивление разрушению керамики YBa2Cu3O7-x
в зависимости от особенностей релаксации
напряжений вблизи развивающеся трещины вследствие переключения сегнетоэластических
доменов.
ТЕРМОДИНАМИКА МАРТЕНСИТНОГО ПРЕВРАЩЕНИЯ
При
окислительном отжиге ВТСП на кривой зависимости кислородного параметра
(x) от времени (t)
наблюдаются два характерных участка. На начальном "быстром"
этапе процесса, где накопление купратом кислорода идет в диффузионном режиме
зависимость "x-t" подчиняется
параболическому закону. На последующем "медленном"
участке кинетика реакции определяется релаксацией упругих напряжений, а
окисление идет в режиме: ¶
x/¶ t @
const, то есть по линейному закону [8,
12]. Как было показано в [8]
соединение YBa2Cu3O7-x
обладает "эффектом запоминания формы", что говорит в пользу мартенситного
механизма релаксации напряжений на медленном этапе окисления материала.
Поэтому можно предположить, что снятие внутренних напряжений 2-го рода,
возникающих в окрестности развивающейся макротрещины может происходить
по мартенситному механизму за счет энергетически выгодной перестройки доменной
структуры кристаллитов.
Будем считать, что напряжения, вводимые процессом двойникования являются
сдвиговыми. Нормальные напряжения, существенные при рассмотрении микрорастрескивания
границ [9] вносят вторичный вклад в
энергию пластической деформации и в даном исследовании не учитываются.
Определим критическое число двойников h
с в сферическом зерне радиуса R,
соответствующее мартенситному превращению. Для этого рассмотрим изменения
в термодинамическом потенциале, сопровождающие формирование сдвойникованного
мартенсита. Они включают приращения механического потенциала D
F m,
состоящего из изменения энергии деформации и энергии взаимодействия;
поверхностной работы D
FS , а
также химического потенциала D
Fc. Последний не
зависит от геометрических параметров двойников и для сферической частицы
радиуса R изменение химической
свободной энергии в одном кристаллите равно:
DFc = - (4.3)pR3DF0 (1)
здесь
DF0 = PV d ij D eijT = PV DV (2)
где PV - напряжение, вызывающее превращение; D eijT - приращения компонент тензора деформации; D V - объемная деформация при превращении [13].
Поверхностная работа определяется изменениями, которые происходят на поверхности раздела мартенсита и при формировании границ двойников. Если протяженность двойника d (см. Рис. 1), то полное изменение поверхностной энергии D F S для сферического зерна есть [7]:
DF S = 4p R2 DG i+ (2/3) p R2 (h - 1) (h + 1) G t / h (3)
где D
G i
- изменение поверхностной энергии,
G t
- энергия двойниковой границы, h
= 2R/d - количество двойников
в одном зерне.
Изменение механической энергии складывается из двух частей:
(1) связанное с двойникованием D
F Tm
и (2) вследствие макроизменения формы
зерна D
F mm.
Компонента, обусловленная двойникованием определяется при исследовании
с помощью метода Эшелби [14] распределения
касательных напряжений, развивающихся в мартенситных пластинах, содержащих
двойники. Тогда при n
= 0.2 (n -
коэффициент Пуассона) имеем [7]:
DFTm = (1.6/3)pR3 GgT2 /h (4)
где G -
модуль сдвига, g
T - деформация сдвига
при двойниковании. Этот член определяется касательными напряжениями, действие
которых ограничивается зоной, близкой к поверхности раздела "родительская
фаза - продукт двойникования". Кроме того, в силу пренебрежения нормальными
напряжениями соотношение (4), можно считать, представляет собою нижнюю
границу возможных значений D
F Tm.
Макроскопическая компонента в случае приложенного напряжения pijA
включает энергию деформации и энергию
взаимодействия с приложенным напряжением. Ограничимся только дилатационной
составляющей приложенного напряжения pA (пренебрегая
девиаторной компонентой), в силу того, что хотя трансформированные частицы
и содержат ряд плоскостей, сформированных сдвигом, всегда существуют альтернативные
плоскости, подвергающиеся сдвигу противоположного знака. Поэтому заметные
макроскопические сдвиговые деформации, по-видимому, трудно ожидать в случае
конечного числа двойников. Тогда D
Fmm
имеет вид [15]:
DFmm = (4/3) p R3 DV (0.14 EDV - pA) (5)
где E = 2G(1 + n) - модуль Юнга. Из соотношений (1), (3) - (5) выразим изменение полного потенциала, связанного с превращением:
![]() =
= ![]() +
+![]()
![]() +
+ ![]() +
+ ![]() 2
--
2
-- ![]() +
+ ![]() (6)
(6)
Таким образом, превращение будет определяться
четырьмя основными параметрами: химической
свободной энергией (D
F0), размером зерна
(R), протяженностью двойников
(d) и приложенной дилатационной комронентой
напряжения (pA).
Для оценки критического значения h
с = 2Rс / d, соответствующего превращению
(Rc - критический
размер зерна) приравняем изменение полного потенциала D
F к нулю.
При этом условии обеспечивается минимальное значение критического числа
доменов в одном зерне h
с при котором будет начинаться превращение. Тогда из
(6) имеем:
![]() +
+![]()
![]() +
+ ![]() +
+ ![]() -
- ![]() +
+ ![]() = 0
(7)
= 0
(7)
Далее представим протяженность двойника d на основе моделирования источников напряжений на границах полидоменных зерен непрерывно - распределенными дислокациями в виде [2]:
![]() (8)
(8)
здесь S0 - спонтанная деформация сдвига; s d - энергия 900 - ной доменной стенки. Отметим, что корневая зависимость d ~ R1/2 также была предсказана для частично-стабилизированного ZrO2 при R >> d [7]. Кроме того, критический размер зерна R*, ниже которого двойникование доменов происходить не может, определяется из условия: R = d. Отсюда имеем:
![]() (9)
(9)
Это значение соответствует зерну, не имеющему достаточной упругой энергии для оказания существенного воздействия на согласование доменной стенки, обладающей энергией s d . Подставляя (8) в (7) и полагая pA = 0 (отсутствие приложенных напряжений), окончательно получим уравнение для определения критического значения h с.
УПРОЧНЕНИЕ КЕРАМИКИ
В настоящее время при исследовании процесов разрушения в рамках микроструктурной механики разрушения особое значение имеет рассмотрение устойчивого (докритического) развития трещины. В отличие от неустойчивого распространения (катастрофического разрушения), подчиняющегося классической теории Гриффитса, оно может учесть присущие структуре данного материала внутренние механизмы сопротивления разрушению и, по существу, определяет истинные прочностные характеристики. В терминах силового подхода, с использованием КИН заданной моды разрушения (I, II, III или их комбинации) соотношения, определяющие равновесные состояния развития трещины на указанных стадиях ее распротранения, имеют вид [16]:
dK/dc > dKс/dc, при неустойчивом разрушении (10.1)
dK/dc < dKс/dc, при устойчивом разрушении (10.2)
где с - длина развивающейся трещины; Kс - критическое значение коэффициента интенсивности напряжений, определяющее страгивание трещины (трещиностойкость керамики). Если существуют внутренние механизмы, вносящие вклад в движущую силу трещины, то эффективная движущая сила, действующая в вершине трещины (К) может быть представлена суммой приложенной внешней нагрузки (Ка) и внутренних воздействий (Кi):
К = Ка
+ ![]() (11)
(11)
Далее, размер зоны превращений rс
может быть найден из соотношения (14) при К = Кс и максимальном
значении достижимой вязкости (при Q »
p /3) [6, 18].
Последнее предполагает, что каждая частица подвергается достаточному сдвиговому
напряжению, вводящему мартенситное превращение, при условии выполнения
термодинамического ограничения (7) (при pA = 0),
наложенного на нее. Отметим, что значение угла
Q»p/3
разделяет зоны упрочнения и уменьшения сопротивления разрушению материала
в окрестности вершины трещины. Трансформировавшиеся частицы на фронте трещины
увеличивают Ktip (концентрацию
напряжений при вершине трещины), в то время как частицы, лежащие в области
Q >
p/3 приводят
к обратному эффекту.
Наконец рассмотрим упрочнение (увеличение сопротивления разрушению) СК
вследствие процессов двойникования в зоне процесса шириной 2rс,
окружающей развивающуюся трещину (см. Рис. 2). Учитывая поведение СК, вызванное
гистерезисом кривой "напряжение-деформация"
(s -e),
можем оценить упрочнение при устойчивом состоянии распространения трещины,
которое определяется двойникованием, следующим [3, 19]:
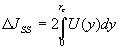 -
повышение сопротивления разрушению; U - площадь
под кривой "s-e",
определяемая в каждой точке с координатой
y на основе определяющего закона
для материала, подвергающегося двойникованию. Или для одноосной кривой
"s -e"
(15) окончательно приводится к виду [3]:
-
повышение сопротивления разрушению; U - площадь
под кривой "s-e",
определяемая в каждой точке с координатой
y на основе определяющего закона
для материала, подвергающегося двойникованию. Или для одноосной кривой
"s -e"
(15) окончательно приводится к виду [3]:
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И ВЫВОДЫ
Для
получения численных результатов использовались известные параметры YBa2Cu3O7-x:
G = 41 ГПа, gТ
~S0 = 0.018,
Gt ~sd
= 0.01 Дж/м2
[7]. Более подробно остановимся на выборе
значений объемной деформации D
V и порогового напряжения s
0 (PV). Как
показано в [20] в результате структурного
фазового перехода при температуре TS = 920K
из тетрагональной фазы (P4/mmm)
в орторомбическую (Pmmm) возникает
спонтанная (неупругая) деформация, определяемая компонентами C22,
C23 и С55
матрицы упругих жесткостей, а ниже TS (в
орторомбической фазе) сформированная доменная структура СК может переключаться
из одного спонтанно-деформируемого ориентационного состояния в другое внешним
сдвиговым воздействием s
. При s
= sс,
где sс -
коэрцитивное напряжение, модуль сдвига достигает минимума, так как в этом
случае число двойников максимально и образец наиболее податлив к механическому
воздействию. С увеличением s
>sс
число двойников уменьшается, приводя к
большей жесткости образца и возрастанию G.
В связи с этим будем выбирать в качестве порогового значения s0
= sс.
Представленные в [20] температурные зависимости sс
в окрестности структурного фазового перехода
дают значение s
с @ 3
МПа. Это гораздо меньше соответствующего значения порогового напряжения,
вызывающего двойникование (20 МПа), которое получено в работе [21]
для образцов BaTiO3,
испытанных на ударную нагрузку при различных скоростях нагружения и величины,
найденной для частично-стабилизированного ZrO2
(4 ГПа) [13].
Наконец, скачок спонтанной деформации при фазовом переходе будем полагать
равным D
V = 10-4 в соответствии
с имеющимися экспериментальными данными [20]. Это
также намного меньше соответствующих значений для BaTiO3
(54x10-4) [22] и для
ZrO2 (57x10-3) [13].
Подставим необходимые величины в уравнение (7) (при pA =
0), предварительно находя значения протяженности
двойников d из соотношения (8)
для различных действительных размеров зерен СК R = 10 - 100
мкм. Решение (7) для указанного
интервала изменения размеров зерен дает значения h
с очень близкие к нулю. Тогда
из (14) и (15) следует отсутствие реального упрочнения СК, обусловленного
процессами двойникования. Это объясняется очень низкими значениями D
V и PV,
определяющими спонтанную деформацию в СК по
сравнению с соответствующими величинами для частично-стабилизированного
ZrO2 [13] и сегнетокерамики
BaTiO3 [21, 22], где
процессы двойникования играют главную роль в упрочнении материала. Таким
образом, упрочнение при разрушении сверхпроводящей керамики YBa2Cu3O7-x,
обусловлено микрорастрескиванием вследствие анизотропии КТР зерен и связанными
с ним процессами (в частности, ветвлением и мостикообразованием за фронтом
макротрещины [9]), а не превращениями мартенситного типа.
ЛИТЕРАТУРА
1.Arlt G. - J. Mater. Sci., 1990, V.25, P.2655.
2.Перцев Н.А., Арльт Г.-ФТТ, 1991, Т.33,
С.3077.
3.Deve H.E., Evans A.G.- Acta Metall. et Mater., 1991, V.39, P.1171.
4.Karpinsky D.N., Parinov I.A.- Ferroelectric Lett, 1995, V.19, N5/6,
P.151.
5.Parinov I.A.- Ferroelectrics, 1995, V.172, P.253.
6.Evans A.G., Cannon R.M. - Acta Metall., 1986, V.34, P.761.
7.Evans A.G., Burlingame N., Drory M., Kriven W.M. - Acta Metall.,
1981, V.29, P.447.
8.Фетисов А.В., Фотиев А.А.- СФХТ, 1992,
Т.5, С.1071.
9.Паринов И.А., Паринова Л.В. - СФХТ,
1994, Т.7, С.80.
10.Parinov I.A.- Cryogenics, 1992,
V.32, P.448.
11.Parinov I.A.- unpublished.
12.Фетисов В.Б., Фетисов А.В., Фотиев
А.А.- СФХТ, 1990, Т.3, С.2627.
13.Porter D.L., Evans A.G., Heuer
A.H. - Acta Metall., 1979, V.27, P.1649.
14.Эшелби Дж. Континуальная теория дислокаций.-
М.: Изд-во Иностр. Литер., 1963.- 156с.
15.Evans A.G., Heuer A.H. - J.
Am. Ceram. Soc., 1980, V.63, P.241.
16.Mai J.-W., Lawn B.R.- An. Rev. Mater. Sci.,1986, V.16, P.415.
17.Parinov I.A.- Ferroelectric Lett, 1995, V.19, N5/6, P.157.
18.Marshall D.B., Drory M., Evans A.G.- Fract. Mech. Ceram., 1983,
V.6, P.289.
19.Budiansky B., Hutchinson J.W., Lambropolous J.- Int. J. Solids Struct.,
1983, V.19, P.337.
20.Гриднев С.А., Иванов О.Н.- СФХТ, 1992,
Т.5, С.1143.
21.Крамаров С.О., Дашко Ю.В.- Проблемы
прочности, 1987, N10, C.52.
22.Писаренко Г.Г. Прочность пьезокерамики.-
Киев: Наукова Думка, 1987.- 232с.
ПОДПИСИ ПОД РИСУНКАМИ
Рис.1. (а) Несдерживаемая форма частицы до начала двойникования; направления растяжения и сжатия вдоль главных осей, характеризующих превращение показаны стрелками; (б) та же частица после завершения двойникования (g т - угол сдвига, d - протяженность двойника); (в) восстановление начальной формы с помощью однородных касательных напряжений t = G gт / 2, показанных стрелками.
Рис.2. Эффект зоны превращений, развивающейся в окрестности трещины (1) на упрочнение керамики: (а) фронтальная и (2) следовая (3) области упрочнения (указанные на рисунке параметры расшифрованы в тексте); (б) изменение вязкости, связанное с местоположением трансформирующейся частицы во фронтальной зоне превращений (D К - приращение КИН, обусловленное превращением, D К* - изменение интенсивности напряжений, вследствие полного развития зоны превращений, то есть при больших значениях D с/rc) [6].