I. A. Parinov

Mechanics and Applied Mathematics Research Institute, Rostov State University, Rostov-on-Don, 344090, Russia

Three sub-problems which are able to advance the problem of an optimization of the manufacture techniques and high-temperature superconducting (HTSC) compositions, namely: (i) a yield criterion which can describe both the bulk movement and the consolidation of powder in a compaction process, (ii) a carbon segregation which embrittles intergranular boundaries, and (iii) a void transformation during sintering, are considered. In the proposed yield criterion, an effect of volume change on the strain of the powder during the compaction process is considered by adding the first invariant of stress tensor in the criterion. The carbon segregation processes are associated with slow, fast and steady states of the dislocation-screened crack growth. The phenomenological models of pore drag, shrinkage, coarsening and coalescence at the grain boundaries and a possible pore breakaway are developed by considering the third sub-problem.

HTSC, compaction, sintering, damage, yield, carbon, diffusion

It is obviously, that an optimization of the manufacture techniques and material compositions is the most important to obtain HTSC with improved and more controlled structure-sensitive properties. The techniques used to prepare the HTSC bulks are very complex and usually include some intermediate stages, the goal of which is to obtain a highly connected and align grain structure. During concrete thermal and pressing treatments the secondary phases and segregations form into the composition, rendering, generally, non-simple effect on the final HTSC properties. For example, the melt-processing has been successfully applied to prepare the large-grain superconductive YBa₂Cu₃O_7-x (YBCO) ceramics with decreased content of the intergranular boundaries and improved critical current density (J_c) [1]. However, there are great problems connected with preparation of the optimum compositions, thermal and pressing regimes. Then, in order to rise J_c into (Bi, Pb)₂Sr₂Ca₂Cu₃O₁₀ (Bi-2223) compositions a silver dispersion is inserted into calcinated powder and the intermediate cold or hot pressings are fulfilled [1]. At the same time, there is considerable problem of carbon which segregates to the intergranular boundaries and embrittles them.

It is the aim of this paper to consider the next sub-problems which could help to improve the processing techniques and compositions for above HTSC systems: (i) a yield criterion which can describe the bulk movement and the consolidation of powder in a compaction process, (ii) a carbon segregation which embrittles intergranular boundaries, and (iii) a void transformation during sintering.

The computer models of the structure sintering, shrinkage, cooling and also the grain recrystallization for different YBCO and Bi-2223 compositions have been developed by using the finite difference method and Monte-Carlo procedures [2-6]. The more powerful finite element methods need detailed information on the critical characteristics and microstructure features. During the powdered HTSC compaction the mechanism of densification involves two processes, namely bulk movement and plastic deformation of particles. Because of the compact consists of numerous particles, one may be considered as a homogeneous continuum. Then, it is necessary to find a limiting condition or a yield criterion to describe the deformation during the compaction. Successful yield criterion is able to help in advance to optimum HTSC compositions. The deformation due to a grain slip results to an increase of volume in the compaction, while the yielding due to a consolidation leads to a volume decrease. At the transition point or critical state, the volume remains constant. Various yield criteria for the loose, porous and granular materials have been reviewed. However, as rule, these criteria do not take into account the effect of density on deformation. Moreover, due to the volume inconstancy during compaction the effect of hydrostatic pressure should be included in the yield criterion. At the same time, the limiting envelopes, stated by the Mohr-Coulomb's and related criteria, suggest an infinitely large shear stress to cause slip at compression, but this is not applied to granular materials. Therefore, the yield criterion for powdered compaction should suppose a closed limiting envelope (e.g., in the elliptic form), with asymmetrical conditions of the compressive and tensile stresses, because powders are not able to sustain tensile loading. Following to [7], for isotropic case of the powdered HTSC compaction it is considered 3D yield criterion in the form

(1)

where a , b and s are the material constants depended on the sample density, Y is the yield stress of the fully dense material, I₁ and I₂ are the first and second invariants of the stress tensor, respectively. Eqn. 1 can be represented in the terms of normal (s ) and shear (t ) stresses as

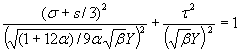(2)

By using the yield function f as the plastic potential, the associated flow rule is obtained from the normality condition between the plastic strain increments, and the yield surface in the form

(3)

where is the Kronecker delta, and are the hydrostatic and deviatoric stresses, respectively. Find the proportionality constant, , from Eqns. 1 and 3 as , where and are the volumetric and deviatoric strain increments. The material constants a , b and s can be found from the shear test [8]. For this, the yield locus is represented at the s - t plane by the ellipse with Eqn. 2. Due to the assumption of isotropic deformation the transition point approximately coincides with the apex of the minor axis of the ellipse. Then the inclined angle (y ) of the critical state line against the abscissa (s ), and the ratio (R ) of the ellipse major axis to the minor one can be treated as material constants, and from Eqn. 2 they have forms: and . Finally, as the third necessary equation we take the dependence between the density of a powder compact and pressure needed to achieve that density [9], namely: , where P is the applied pressure, r ₀ and r are the average densities of the loose powder and the presspowder, respectively, and K is an experimental constant. Then, taking into account the relationship: , the experimental constants y , R and K can be used to determine the values of a , b and s as

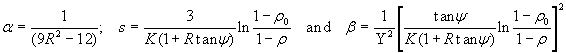. (4)

A satisfactoriness of the proposed criterion to compaction of the HTSC precursors can be verified by using, e.g. the triaxial compaction test. However, it should be noted, that the triaxial compaction tests of sand, concrete and rock have shown that associated plasticity cannot describe experimental data satisfactorily [10]. At the same time, this issue has not been discussed for the powdered HTSC compaction.

Carbon can be introduced into yttrium and bismuth HTSC ceramics by carbon-containing gases or liquids. During the processing it is possible to form nanometer-scale carbon inclusions with superconductor grains and enhance flux pinning substantially [11]. However, it is well known, that carbon or carbon dioxide segregated to the grain boundaries can degrade them and transport properties, respectively [12]. The segregation processes can be studied by using the microscopic models of the equilibrium slow and fast propagation, and also a steady state growth of a dislocation-screened crack.

Consider an intergranular crack with the length, 2a, in a carbonated HTSC. The crack lies along x axis in an elastic-plastic isotropic body with shear modulus, G, Poisson ratio, n , yield strength, s _y, and work hardening factor, n. The body is loaded by a remote stress, s _a, parallel to the y axis at a constant temperature, T. At the x axis two linear dislocation arrays with the length r_y locate at the distance d from the crack tips. It is assumed, the size of the arc-shaped crack tips, q, remains constant during plastic deformation. The condition of the local equilibrium at the crack tip is that one must be screened by dislocation field and maintains a dislocation free zone with the size d. The loaded system "crack - dislocation arrays" maintains a local stress, s _d, in the dislocation free zone and produces the next stress intensity [13, 14]

where K_a is the applied stress intensity, and b is the factor depended on the elastic and plastic deformation properties. The carbon segregation is found by the crack tip profile and the stress field ahead of the crack tip. The chemical potentials of C and HTSC can be stated following to [15] in various interface zones, namely: I - zone not affected by the stress intensity (ç x ç > a+d+r_y), II - zone of screening dislocations (a+d < ç x ç < a+d+r_y), III - dislocation free zone ahead of the crack tip (a < ç x ç < a+d), IV - arc-shaped crack tip zone (a-q < ç x ç < a) and V - parallel flat crack surface zone (ç x ç < a-q). At equilibrium, the chemical potentials of carbon and superconductor must be the same in the all regions. So, the equilibrium carbon segregation depends on the binding energies and crack tip conditions. The binding energies of C at grain boundaries and crack surfaces (H_B)_b and (H_B)_s, respectively, are found by the standard chemical potentials of C and HTSC as

. (6)

Here and further the subscripts of different parameters indicate the next: m is the matrix, b is the grain boundary, and s is the crack surface. The basic assumption of the model is that the embrittlement occurs as a reduction of the interface energies due to the carbon segregation. Moreover, it is taken into account that slow and fast fractures occur by maintaining the constant chemical potentials and the same carbon concentration between the crack surface and the grain boundary, respectively. Then, from the thermodynamic theory of [16, 17] it can be obtained the variation of the ideal works, expended in slow (g ^s) and fast (g ^f) fracture as

and (7)

where the equilibrium carbon concentrations at zones III and V have forms

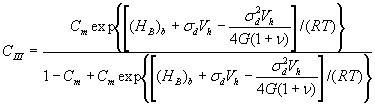and (8)

here C_m is the bulk carbon concentration, V_h is the molar volume of carbon, R is the gas constant, 1/W _i is the carbon coverage at interfaces, and are the critical values of carbon concentration at zone III required, for slow and fast fracture, respectively, g ₀ is the ideal work of intergranular fracture in the absence of carbon, and D m is the chemical potential difference between the crack surface and the stressed grain boundary. The equations for constant carbon concentrations also can be found at zones I and IV. At the same time, due to the variable stress distribution (see Eqn. 5) the carbon content at zone II is not constant. The relationship between critical stress intensity required to propagate the crack (for slow, fast or steady state fracture) and the ideal work change due to the carbon segregation is stated by using the local energy balance condition [15]: , where K_d is the local stress intensity factor, connected with the dislocation free zone ahead of the crack tip (d) and local stress (s _d) in this zone by the equation p d = (K_d /s _d)², the superscript c corresponds to definite fracture state. Then the threshold stress intensity, , is given by [15]

(9)

where K₀ is the fracture toughness, is the critical crack opening displacement (CCOD) required for various fracture processes (superscript c), and d _c0 is the CCOD in the absence of carbon, defined as

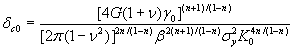(10)

Assume, that the carbon diffusion along stressed boundaries and crack surfaces is the mechanism that controls the intergranular embrittlement and affects the crack growth rate. By this, the bulk diffusion effects are neglected. Under the geometrical and loading conditions of above considered equilibrium crack growth problem, the steady state case indicates the crack growth with constant velocity. Taking into account the five grain boundary and crack surface zones (I-V) the fluxes of carbon in these regions, , can be stated as

(11)

where D_i is the diffusivity of carbon, is the carbon concentration, i is the subscript indicating b or s, and j is the superscript indicating various interface zones, are the corresponding chemical potentials. The differentiation with respect to s is carried out only at zone IV, by this, s is the variable arc length at the correspondent part of the arc-shaped crack tip. The continuity equation of fluxes is

(12)

where t is the time. Based on the Eqns. 5, 11 and 12, and also the relationship between the interface energies, , and the amounts of carbon, , in the various zones, derived from the Gibbs theory and dilute solute approximation as , the second-order differential equations, controlling the carbon diffusion in the intergranular cracking regions, can be obtained, analogously to [18]. It is assumed, the steady state crack growth maintains the equilibrium values at the crack center and at the triple point of grain boundaries ahead of the crack. The interface conditions find that the chemical potentials and fluxes of carbon must be the same at each interface in order to maintain the continuity of the carbon flux. So, it is stated the boundary value problem for solution of which some relationships defined in the equilibrium crack growth are used. The carbon effect is determined by the ideal work of steady state fracture as

(13)

where and ,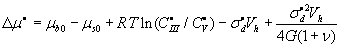

the superscript indicates the steady state fracture. The boundary value problem can be solved numerically, e.g. by using the Runge-Kutta method. The boundary conditions at the triple points allow to study the effects of grain sizes. Then, the model of the steady state crack growth caused by the carbon segregation can be added to previously developed modeling of the toughening mechanisms, acting into HTSC structures [3-6]. At the same time, the size effects can not be estimated in the cases of the equilibrium slow and fast cracks.

As it has been shown in [19] the critical current in the monofilamentary Bi-2223/Ag tape, at first, increases with annealing time, attains maximum value and then decreases with reaction time. This behavior has been connected by authors with action of competing mechanisms, which initially improve the grain boundary quality and then lower pinning strength. The last has been explained by the lead expelling during sintering. However, during BSCCO/Ag tape processing considerable porosity due to CO₂ release can be observed, in particular leading to bubbles arising and the critical current decrease. For example, 200 ppm of carbon has caused up to 36% porosity in the core of Bi-2212/Ag tapes [12]. In the phenomenological analysis the grain growth and corresponding motion of pores located initially at triple grain junctions are assumed. The complete separation of a pore from a grain boundary occurs after the pore displacement at two-grain interface. It is accompanied by the grain disappearance and coalescence of the triple grain junction pores during the grain growth. The motion of the pore together with grain boundary takes place because of inducing a flux of atoms from leading to trailing surface of the pore. This approach allows to describe different pore motions accompanying grain growth, namely pore drag, shrinkage, coarsening, coalescence and breakaway. Though a grain size observed in the monocore Bi-2223/Ag tapes has remained constant during various durations (from 40 to 240 hours) of annealing [19], nevertheless, the grain size distribution should be different in the various cases. This is supported by considerable lead expelling monotonously increasing with annealing time [19]. But then these additions heterogeneously distributed into material can inhibit only a local grain growth in the Bi-2223 core. Moreover, the phenomenological analysis has shown, that for shrinkage of grain boundary pores and averting of pore separation there are two main conditions: (i) a small grain boundary mobility, and (ii) a large boundary diffusivity. However, simultaneously both these conditions can only be satisfied in the presence of appreciable addition drag, throughout the grain disappearance process. Finally, as it has been shown in the modeling of fracture processes in YBCO the size distributions play more important role to compare with the mean sizes [4]. Hence, a preservation of the grain size value in the different annealing times, generally does not allow to assert an absence of grain growth and microstructural alterations. In discussion of pore breakaway, at first it should be noted, that a pore attached to a grain boundary decreases due to grain boundary diffusion, but when the pore separates from the grain boundary and displaces into grain, one can shrinkage only thanks to much more slow diffusion of crystalline lattice. Further, the steady growth of a pore is possible at the dihedral angles of Y < p , and the pore stability rises with decrease of Y. In Bi-2223 core there is a spectrum of dihedral angles, connected with various grain boundary structures which form during processing. This spectrum corresponds to critical size interval of pores, as rule located at the low angle boundaries (those especially are character for Bi-2223/Ag tapes, where effective misalignment angle between grains is equal to approximately 7.5^o [19]). Then, the distributions of different diffusivities and grain boundary mobilities exist thanks to heterogeneous distributions of additions. The material and structure property changes which suppress pore separations can be estimated by comparing the critical pore size with trajectories of pore and grain sizes at the final stage of annealing. The approach developed allows to determine intervals of pore size change for avoidance of pore separation. It is most desirable behavior in annealing when grain boundary mobility, initial pore size (a₀) and boundary diffusivity are very small. In this case a peak size of pore for the process of pore and grain coarsening coincides with initial pore size in precursor sample. Then the pore coarsening excludes during annealing. In other case, it is necessary to consider processes of optimum pore coarsening and averting of pore separation. The phenomenological analysis states that a lower limit for pore separation size, a_c, at all reasonable values of  a₀/R (where R is the grain radius) is given by , where D_sd_s is the surface diffusion parameter, W is the atomic volume, g_s and g_b are the surface and grain boundary energies, respectively, M_b is the grain boundary mobility, k is Boltzmann constant, T is the annealing temperature. By selecting above parameters as following [19, 20]: W = 2.2*10^-30 m³, D_sd_s = 2.5*10^-21 m³/s, g_s = 2g_b, Y_max = p/2, T = 1110K (here some parameters have been taken for Al₂O₃, because of their absence for Bi-2223), we obtain a very high value of  M_b @ 7000m/(Ns) even for a_c = 100nm. More grain mobility is demanded for less pores separated from grain boundary. Obviously, the size of pores which can separate from grain boundaries during annealing on some orders of value more than coherence length ( @ 1nm) in Bi-2223. Then, these separated pores can not serve as effective pinning centres and because of percolation features they must considerably diminish the critical current. Thus, the lead expelling causes a decrease of critical current in long reaction, but rather due to pore transformations occured during calcination, than thanks to decrease of the pinning efficiency in the grains, assumed in Ref. [19].

So, the solutions obtained in this paper can be used in the finite element formulations by which the stress-strain states and damage parameters during compaction and sintering of the HTSC powders can be predicted.

This work was supported by the Russian Department of Common and Professional Education (Program of Basic Researches in Physics).

1. S. Sengupta (1998) JOM 50, 19.
2. I. A. Parinov (1992) Cryogenics 32, 448.

3. I. A. Parinov and L. V. Parinova (1994) Supercond. Phys. Chem. Techn. 7, 79.

4. I. A .Parinov , E. V. Rozhkov and C. E. Vassil'chenko (1997) IEEE Trans. Appl. Supercond. 7, 1941.

5. I. A. Parinov , E. V. Rozhkov and C. E. Vassil'chenko (1998) Adv. Cryog. Eng. (Mater.). 44b, 639.

6. I. A. Parinov and Y. A. Kozinkina (1998) Adv. Cryog. Eng. (Mater.). 44b, 449.

7. F.-K. Chen (1998) Appl. Mech. Eng. 3, 413.

8. H. Tsunakawa and R. Aoki (1982) Powder Tech. 33, 249.

9. R. W. Heckel (1961) Trans. Metal. Soc. AIME 221, 671.

10. P. A. Vermeer (1998). In: Physics of Dry Granular Media, pp. 163-195, Herrmann, H. J., Hovi, J.-P. and

Luding, S. (Eds). Kluwer Academic Publishers, Dordrecht.

11. S. Sengupta, V. R. Todt, K. C. Goretta, et al. (1997) IEEE Trans. Appl. Supercond. 7, 1727.

12. W. Zhang, M. Polak, A. Polyanskii, et al. (1998) Adv. Cryog. Eng. (Mater.). 44b, 509.

13. J. W. Hutchinson (1968) J. Mech. Phys. Solids. 16, 13.

14. J. R. Rice and G. F. Rosengren (1968) J. Mech. Phys. Solids. 16, 1.

15. J. Kameda (1986) Acta Metall. 34, 867.

16. M. P. Seah (1976) Proc. R. Soc. Lond. A349, 539.

17. J. P. Hirth and J. R. Rice (1980) Metall. Trans. A. 11A, 1809.

18. J. Kameda (1986) Acta Metall. 34, 883.

19. F. Marti, G. Grasso, J.-C. Grivel and R. Flukiger (1998) Supercond. Sci. Technol. 11, 485.

20. J. R. Porter, W. Blumenthal and A. G. Evans (1981) Acta Metall. 29, 1899.